By this time there were already suspicions that these atoms were not, after all, indivisible. Several years previously a fellow of Trinity College, Cambridge, J. J. Thomson, had demonstrated the existence of a particle of matter, called the electron, that had a mass less than one thousandth of that of the lightest atom. He used a setup rather like a modern TV picture tube: a red-hot metal filament gave off the electrons, and because these have a negative electric charge, an electric field could be used to accelerate them toward a phosphor-coated screen. When they hit the screen, flashes of light were generated. Soon it was realized that these electrons must be coming from within the atoms themselves, and in 1911 the New Zealand physicist Ernest Rutherford finally showed that the atoms of matter do have internal structure: they are made up of an extremely tiny, positively charged nucleus, around which a number of electrons orbit. He deduced this by analyzing the way in which alpha-particles, which are positively charged particles given off by radioactive atoms, are deflected when they collide with atoms.
At first it was thought that the nucleus of the atom was made up of electrons and different numbers of a positively charged particle called the proton, from the Greek word meaning “first,” because it was believed to be the fundamental unit from which matter was made. However, in 1932 a colleague of Rutherford’s at Cambridge, James Chadwick, discovered that the nucleus contained another particle, called the neutron, which had almost the same mass as a proton but no electrical charge. Chadwick received the Nobel Prize for his discovery, and was elected Master of Gonville and Caius College, Cambridge (the college of which I am now a fellow). He later resigned as Master because of disagreements with the Fellows. There had been a bitter dispute in the college ever since a group of young Fellows returning after the war had voted many of the old Fellows out of the college offices they had held for a long time. This was before my time; I joined the college in 1965 at the tail end of the bitterness, when similar disagreements forced another Nobel Prize – winning Master, Sir Nevill Mott, to resign.
Up to about thirty years ago, it was thought that protons and neutrons were “elementary” particles, but experiments in which protons were collided with other protons or electrons at high speeds indicated that they were in fact made up of smaller particles. These particles were named quarks by the Caltech physicist Murray Gell-Mann, who won the Nobel Prize in 1969 for his work on them. The origin of the name is an enigmatic quotation from James Joyce: “Three quarks for Muster Mark!” The word quark is supposed to be pronounced like quart, but with a k at the end instead of a t, but is usually pronounced to rhyme with lark.
There are a number of different varieties of quarks: there are six “flavors,” which we call up, down, strange, charmed, bottom, and top. The first three flavors had been known since the 1960s but the charmed quark was discovered only in 1974, the bottom in 1977, and the top in 1995. Each flavor comes in three “colors,” red, green, and blue. (It should be emphasized that these terms are just labels: quarks are much smaller than the wavelength of visible light and so do not have any color in the normal sense. It is just that modern physicists seem to have more imaginative ways of naming new particles and phenomena – they no longer restrict themselves to Greek!) A proton or neutron is made up of three quarks, one of each color. A proton contains two up quarks and one down quark; a neutron contains two down and one up. We can create particles made up of the other quarks (strange, charmed, bottom, and top), but these all have a much greater mass and decay very rapidly into protons and neutrons.
We now know that neither the atoms nor the protons and neutrons within them are indivisible. So the question is: what are the truly elementary particles, the basic building blocks from which everything is made? Since the wavelength of light is much larger than the size of an atom, we cannot hope to “look” at the parts of an atom in the ordinary way. We need to use something with a much smaller wave-length. As we saw in the last chapter, quantum mechanics tells us that all particles are in fact waves, and that the higher the energy of a particle, the smaller the wavelength of the corresponding wave. So the best answer we can give to our question depends on how high a particle energy we have at our disposal, because this determines on how small a length scale we can look. These particle energies are usually measured in units called electron volts. (In Thomson’s experiments with electrons, we saw that he used an electric field to accelerate the electrons. The energy that an electron gains from an electric field of one volt is what is known as an electron volt.) In the nineteenth century, when the only particle energies that people knew how to use were the low energies of a few electron volts generated by chemical reactions such as burning, it was thought that atoms were the smallest unit. In Rutherford’s experiment, the alpha-particles had energies of millions of electron volts. More recently, we have learned how to use electromagnetic fields to give particles energies of at first millions and then thousands of millions of electron volts. And so we know that particles that were thought to be “elementary” thirty years ago are, in fact, made up of smaller particles. May these, as we go to still higher energies, in turn be found to be made from still smaller particles? This is certainly possible, but we do have some theoretical reasons for believing that we have, or are very near to, a knowledge of the ultimate building blocks of nature.
 Using the
wave/particle duality discussed in the last chapter, every-thing in the
universe, including light and gravity, can be described in terms of particles.
These particles have a property called spin. One way of thinking of spin is to
imagine the particles as little tops spinning about an axis. However, this can
be misleading, because quantum mechanics tells us that the particles do not
have any well-defined axis. What the spin of a particle really tells us is what
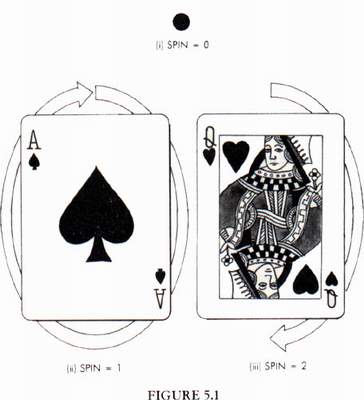
the particle looks like from different directions. A particle of spin 0 is like
a dot: it looks the same from every direction (Fig. 5.1-i). On the other hand,
a particle of spin 1 is like an arrow: it looks different from different
directions (Fig. 5.1-ii). Only if one turns it round a complete revolution (360
degrees) does the particle look the same. A particle of spin 2 is like a
double-headed arrow (Fig. 5.1-iii): it looks the same if one turns it round
half a revolution (180 degrees). Similarly, higher spin particles look the same
if one turns them through smaller fractions of a complete revolution. All this
seems fairly straightforward, but the remark-able fact is that there are
particles that do not look the same if one turns them through just one
revolution: you have to turn them through two complete revolutions! Such
particles are said to have spin ½.
Using the
wave/particle duality discussed in the last chapter, every-thing in the
universe, including light and gravity, can be described in terms of particles.
These particles have a property called spin. One way of thinking of spin is to
imagine the particles as little tops spinning about an axis. However, this can
be misleading, because quantum mechanics tells us that the particles do not
have any well-defined axis. What the spin of a particle really tells us is what
the particle looks like from different directions. A particle of spin 0 is like
a dot: it looks the same from every direction (Fig. 5.1-i). On the other hand,
a particle of spin 1 is like an arrow: it looks different from different
directions (Fig. 5.1-ii). Only if one turns it round a complete revolution (360
degrees) does the particle look the same. A particle of spin 2 is like a
double-headed arrow (Fig. 5.1-iii): it looks the same if one turns it round
half a revolution (180 degrees). Similarly, higher spin particles look the same
if one turns them through smaller fractions of a complete revolution. All this
seems fairly straightforward, but the remark-able fact is that there are
particles that do not look the same if one turns them through just one
revolution: you have to turn them through two complete revolutions! Such
particles are said to have spin ½.All the known particles in the universe can be divided into two groups: particles of spin ½, which make up the matter in the universe, and particles of spin 0, 1, and 2, which, as we shall see, give rise to forces between the matter particles. The matter particles obey what is called Pauli’s exclusion principle. This was discovered in 1925 by an Austrian physicist, Wolfgang Pauli – for which he received the Nobel Prize in 1945. He was the archetypal theoretical physicist: it was said of him that even his presence in the same town would make experiments go wrong! Pauli’s exclusion principle says that two similar particles can-not exist in the same state; that is, they cannot have both the same position and the same velocity, within the limits given by the uncertainty principle. The exclusion principle is crucial because it explains why matter particles do not collapse to a state of very high density under the influence of the forces produced by the particles of spin 0, 1, and 2: if the matter particles have very nearly the same positions, they must have different velocities, which means that they will not stay in the same position for long. If the world had been created without the exclusion principle, quarks would not form separate, well-defined protons and neutrons. Nor would these, together with electrons, form separate, well-defined atoms. They would all collapse to form a roughly uniform, dense “soup.”
A proper understanding of the electron and other spin-½ particles did not come until 1928, when a theory was proposed by Paul Dirac, who later was elected to the Lucasian Professorship of Mathematics at Cambridge (the same professorship that Newton had once held and that I now hold). Dirac’s theory was the first of its kind that was consistent with both quantum mechanics and the special theory of relativity. It explained mathematically why the electron had spin-½; that is, why it didn’t look the same if you turned it through only one complete revolution, but did if you turned it through two revolutions. It also predicted that the electron should have a partner: an anti-electron, or positron. The discovery of the positron in 1932 confirmed Dirac’s theory and led to his being awarded the Nobel Prize for physics in 1933. We now know that every particle has an antiparticle, with which it can annihilate. (In the case of the force-carrying particles, the antiparticles are the same as the particles themselves.) There could be whole antiworlds and antipeople made out of antiparticles. However, if you meet your antiself, don’t shake hands! You would both vanish in a great flash of light. The question of why there seem to be so many more particles than antiparticles around us is extremely important, and I shall return to it later in the chapter.
In quantum mechanics, the forces or interactions between matter particles are all supposed to be carried by particles of integer spin – 0, 1, or 2. What happens is that a matter particle, such as an electron or a quark, emits a force-carrying particle. The recoil from this emission changes the velocity of the matter particle. The force-carrying particle then collides with another matter particle and is absorbed. This collision changes the velocity of the second particle, just as if there had been a force between the two matter particles. It is an important property of ' the force-carrying particles that they do not obey the exclusion principle. This means that there is no limit to the number that can be exchanged, and so they can give rise to a strong force. However, if the force-carrying particles have a high mass, it will be difficult to produce and exchange them over a large distance. So the forces that they carry will have only a short range. On the other hand, if the force-carrying particles have no mass of their own, the forces will be long range. The force-carrying particles exchanged between matter particles are said to be virtual particles because, unlike “real” particles, they cannot be directly detected by a particle detector. We know they exist, however, because they do have a measurable effect: they give rise to forces between matter particles. Particles of spin 0, 1, or 2 do also exist in some circumstances as real particles, when they can be directly detected. They then appear to us as what a classical physicist would call waves, such as waves of light or gravitational waves. They may sometimes be emitted when matter particles interact with each other by exchanging virtual force-carrying particles. (For example, the electric repulsive force between two electrons is due to the exchange of virtual photons, which can never be directly detected; but if one electron moves past another, real photons may be given off, which we detect as light waves.)
Force-carrying particles can be grouped into four categories according to the strength of the force that they carry and the particles with which they interact. It should be emphasized that this division into four classes is man-made; it is convenient for the construction of partial theories, but it may not correspond to anything deeper. Ultimately, most physicists hope to find a unified theory that will explain all four forces as different aspects of a single force. Indeed, many would say this is the prime goal of physics today. Recently, successful attempts have been made to unify three of the four categories of force – and I shall describe these in this chapter. The question of the unification of the remaining category, gravity, we shall leave till later.
The first category is the gravitational force. This force is universal, that is, every particle feels the force of gravity, according to its mass or energy. Gravity is the weakest of the four forces by a long way; it is so weak that we would not notice it at all were it not for two special properties that it has: it can act over large distances, and it is always attractive. This means that the very weak gravitational forces between the individual particles in two large bodies, such as the earth and the sun, can all add up to produce a significant force. The other three forces are either short range, or are sometimes attractive and some-times repulsive, so they tend to cancel out. In the quantum mechanical way of looking at the gravitational field, the force between two matter particles is pictured as being carried by a particle of spin 2 called the graviton. This has no mass of its own, so the force that it carries is long range. The gravitational force between the sun and the earth is ascribed to the exchange of gravitons between the particles that make up these two bodies. Although the exchanged particles are virtual, they certainly do produce a measurable effect – they make the earth orbit the sun! Real gravitons make up what classical physicists would call gravitational waves, which are very weak – and so difficult to detect that they have not yet been observed.
The next category is the electromagnetic force, which interacts with electrically charged particles like electrons and quarks, but not with uncharged particles such as gravitons. It is much stronger than the gravitational force: the electromagnetic force between two electrons is about a million million million million million million million (1 with forty-two zeros after it) times bigger than the gravitational force. However, there are two kinds of electric charge, positive and negative. The force between two positive charges is repulsive, as is the force between two negative charges, but the force is attractive between a positive and a negative charge. A large body, such as the earth or the sun, contains nearly equal numbers of positive and negative charges. Thus the attractive and repulsive forces between the individual particles nearly cancel each other out, and there is very little net electromagnetic force. However, on the small scales of atoms and molecules, electromagnetic forces dominate. The electromagnetic attraction between negatively charged electrons and positively charged protons in the nucleus causes the electrons to orbit the nucleus of the atom, just as gravitational attraction causes the earth to orbit the sun. The electromagnetic attraction is pictured as being caused by the exchange of large numbers of virtual massless particles of spin 1, called photons. Again, the photons that are exchanged are virtual particles. However, when an electron changes from one allowed orbit to another one nearer to the nucleus, energy is released and a real photon is emitted – which can be observed as visible light by the human eye, if it has the right wave-length, or by a photon detector such as photographic film. Equally, if a real photon collides with an atom, it may move an electron from an orbit nearer the nucleus to one farther away. This uses up the energy of the photon, so it is absorbed.
The third category is called the weak nuclear force, which is responsible for radioactivity and which acts on all matter particles of spin-½, but not on particles of spin 0, 1, or 2, such as photons and gravitons. The weak nuclear force was not well understood until 1967, when Abdus Salam at Imperial College, London, and Steven Weinberg at Harvard both proposed theories that unified this interaction with the electromagnetic force, just as Maxwell had unified electricity and magnetism about a hundred years earlier. They suggested that in addition to the photon, there were three other spin-1 particles, known collectively as massive vector bosons, that carried the weak force. These were called W+ (pronounced W plus), W- (pronounced W minus), and Zº (pronounced Z naught), and each had a mass of around 100 GeV (GeV stands for gigaelectron-volt, or one thousand million electron volts). The Weinberg-Salam theory exhibits a property known as spontaneous symmetry breaking. This means that what appear to be a number of completely different particles at low energies are in fact found to be all the same type of particle, only in different states. At high energies all these particles behave similarly. The effect is rather like the behavior of a roulette ball on a roulette wheel. At high energies (when the wheel is spun quickly) the ball behaves in essentially only one way – it rolls round and round. But as the wheel slows, the energy of the ball decreases, and eventually the ball drops into one of the thirty-seven slots in the wheel. In other words, at low energies there are thirty-seven different states in which the ball can exist. If, for some reason, we could only observe the ball at low energies, we would then think that there were thirty-seven different types of ball!
In the Weinberg-Salam theory, at energies much greater than 100 GeV, the three new particles and the photon would all behave in a similar manner. But at the lower particle energies that occur in most normal situations, this symmetry between the particles would be broken. WE, W, and Zº would acquire large masses, making the forces they carry have a very short range. At the time that Salam and Weinberg proposed their theory, few people believed them, and particle accelerators were not powerful enough to reach the energies of 100 GeV required to produce real W+, W-, or Zº particles. However, over the next ten years or so, the other predictions of the theory at lower energies agreed so well with experiment that, in 1979, Salam and Weinberg were awarded the Nobel Prize for physics, together with Sheldon Glashow, also at Harvard, who had suggested similar unified theories of the electromagnetic and weak nuclear forces. The Nobel committee was spared the embarrassment of having made a mistake by the discovery in 1983 at CERN (European Centre for Nuclear Research) of the three massive partners of the photon, with the correct predicted masses and other properties. Carlo Rubbia, who led the team of several hundred physicists that made the discovery, received the Nobel Prize in 1984, along with Simon van der Meer, the CERNengineer who developed the antimatter storage system employed. (It is very difficult to make a mark in experimental physics these days unless you are already at the top! )
The fourth category is the strong nuclear force, which holds the quarks together in the proton and neutron, and holds the protons and neutrons together in the nucleus of an atom. It is believed that this force is carried by another spin-1 particle, called the gluon, which interacts only with itself and with the quarks. The strong nuclear force has a curious property called confinement: it always binds particles together into combinations that have no color. One cannot have a single quark on its own because it would have a color (red, green, or blue). Instead, a red quark has to be joined to a green and a blue quark by a “string” of gluons (red + green + blue = white). Such a triplet constitutes a proton or a neutron. Another possibility is a pair consisting of a quark and an antiquark (red + antired, or green + antigreen, or blue + antiblue = white). Such combinations make up the particles known as mesons, which are unstable because the quark and antiquark can annihilate each other, producing electrons and other particles. Similarly, confinement prevents one having a single gluon on its own, because gluons also have color. Instead, one has to have a collection of gluons whose colors add up to white. Such a collection forms an unstable particle called a glueball.
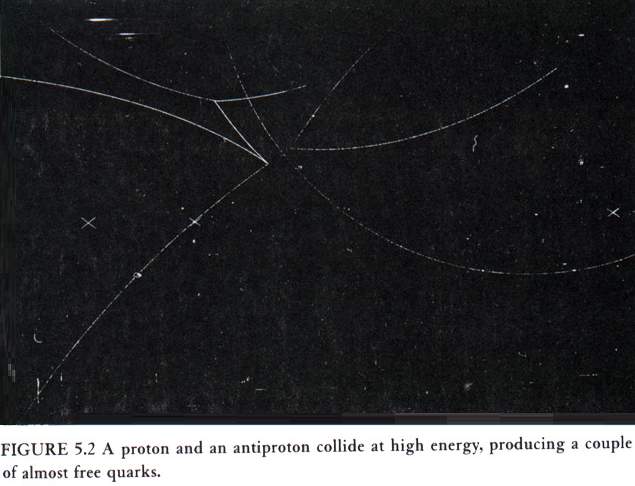
The fact that confinement prevents one from observing an isolated quark or gluon might seem to make the whole notion of quarks and gluons as particles somewhat metaphysical. However, there is another property of the strong nuclear force, called asymptotic freedom, that makes the concept of quarks and gluons well defined. At normal energies, the strong nuclear force is indeed strong, and it binds the quarks tightly together. However, experiments with large particle accelerators indicate that at high energies the strong force becomes much weaker, and the quarks and gluons behave almost like free particles. Fig. 5.2 shows a photograph of a collision between a high-energy proton and antiproton.